
A method of localized, scheduled quantum error correction (Local QEC) developed by researchers at Aliro makes it possible to correct certain errors in an entanglement-based quantum network. In this article, we’ll explain the basics of quantum error correction, and how QEC can be leveraged in an entanglement-based network for more robust connections.
Quantum systems provide novel capabilities and at the same time they also impose restrictions on our ability to leverage these new capabilities. For example, the no-cloning theorem in quantum mechanics states that an arbitrary unknown quantum state can not be copied with high fidelity. This restricts how quantum data can be transmitted. On the other hand, it also prevents adversaries from intercepting quantum communications undetected.
Entanglement is another uniquely quantum phenomenon which is exploited in quantum networking to support secure communication (via teleportation). The quantum processes involved in entanglement generation and distribution are fundamentally stochastic and this constrains the potential performance, necessitating retries and delays within the protocols that result in decoherence and exposure of qubits to environmental noise. Delays can quickly render a qubit(s) unusable by the network as the fidelity (a measure of qubit quality) decays exponentially with time.
These errors can be corrected with Local QEC.
Entanglement-based error correction basics: notation

Dirac notation is used to represent quantum states in the state vector formalism. The main takeaway here is that although this notation may be unfamiliar, what it's really conveying is qubit states as vectors and linear algebra is used to create linear combinations of vectors, to compute inner products, to multiply matrices by vectors, to compute the evolution of the state. The physics is abstracted to linear algebra in all these instances.

There's another, more general state formalism that can be used called the density state formalism. In this case, the states are represented by matrices. Linear algebra is still the root of the mathematics, but the density state formalism is more general, and allows for calculations regarding subsystems of composite systems or noise, or how noise affects the system. It’s much easier to compute these quantities in density state formalism.

Error correction in Entanglement-based Networks: logical qubits and operations

QEC leverages logical qubits. Logical qubits are abstract encoded qubits that are comprised of multiple physical qubits. Logical operations similarly operate on logical qubits, which are composite objects that are created with the encoding. These operations can be thought of as being analogous to the non-encoded forms. They can be used to create superpositions. They can be used to execute gates on logical qubits. However, the underlying operations do involve multiple operations on the individual qubits. The chart above shows a very simple three qubit repetition code. Many error correcting codes become much more complex and involve many more physical qubits than this example. In some architectures, researchers are proposing codes that have hundreds or thousands of physical qubits in the code. Logical qubit operations can be very complex, but the degree of redundancy that is added to the state imparts a greater capability to correct errors. This redundancy is analogous to classical error correction.
Entanglement-based error correction basics: stabilizers

Stabilizers are operations which don't affect the logical state when applied, but can be used to detect errors. The stabilizers are chosen not only to leave the logical state unchanged, but to anti-commute with the errors. Meaning, stabilizers are selected based on the anticipated errors that will likely appear in a system. The takeaway here is that the stabilizer operations are used to detect specific types of errors, depending on which type of error is expected. So if bit flip errors are expected, these errors correspond to X gate operations. In this case Z stabilizers would be used. Conversely, if phase flip errors are anticipated, these are Z gate type errors, and X stabilizers would be used to detect them. In this example, to properly stabilize a state distributed across two nodes, it would be necessary to execute these gates in a synchronized way. In the localized method developed by Aliro, when qubits are logically encoded they can execute their stabilizers independently, which is a major benefit of this localized approach.

Entanglement-based error correction basics: syndrome extraction
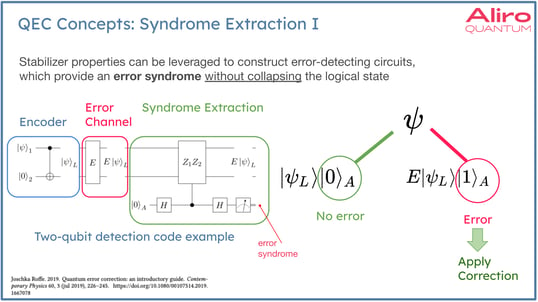
Stabilizer properties can be leveraged to construct error-detecting circuits, which provide an error syndrome without collapsing the logical state. In the diagram to the left, is an encoder. The encoder is the part of a circuit, which will take a raw qubit and encode it into the larger state space. After the state has been encoded, a syndrome extraction circuit can be used to apply stabilizers to detect errors that may have occurred, which the error channel imparted on the system.
What’s happening at a high level here is that the Hadamard gates perform a series of basis transformations, one before and one after the controlled execution of the stabilizer subcircuit, splitting the state into several subspaces. Since the stabilizer operation(s) anti-commune with the expected errors, the “no error” subspace will exhibit constructive interference when there is no error, resulting in a measurement value of zero for the auxiliary qubit. When an error occurs, the “no error” branch collapses due to destructive interference and the “error” branch now exhibits constructive interference, resulting in a measurement value of one for the auxiliary qubit. When an error is detected, the syndrome provides enough information to perform the correction.
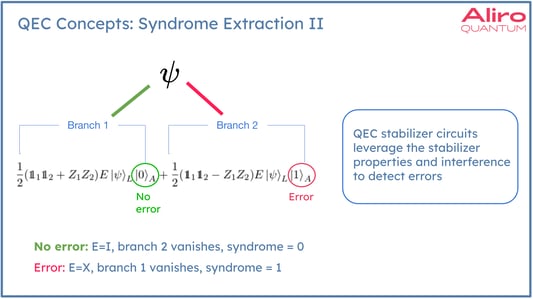
This syndrome extraction is a type of parity check that does not collapse the state. This check can be performed multiple times, and the encoded state remains in superposition. Whenever the state is in the “code space”, it’s not disturbed the stabilizers. In general, stabilizer circuits allow us to leverage the mathematical properties of our stabilizers and interference to detect errors using simple measurements that do not collapse the logical state.
Entanglement-based error correction basics: parameters n, d, k

Another important characterization of QEC codes can be summarized with three different parameters called (n,k,d), where n is the number of physical qubits, k is the number of logical qubits, and d is the code distance. If a code has an (n,k,d) of (3,1,3), that means there are three physical qubits for every logical qubit being encoded. Code distance is related to the number of errors that the code can detect and correct. A code with distance three can detect d - 1 error, 2 errors in this case. In this example, n can correct (d - 1) / 2 , which equals one in this example. There is no code that can detect or correct an arbitrarily large number of errors. Every code has this kind of capacity for error detection and correction.
Quantum Secure Communication in an entanglement-based network
The goal of an entanglement-based quantum network is to distribute entanglement between users across the network. These users may be located some distance from each other and therefore, this entanglement may span multiple repeaters. The entanglement is a resource provided by the network for the purpose of data transmission using a technique called teleportation.
For example: Alice and Bob have pre-established entanglement between them, and Alice would like to teleport another qubit which is labeled qC in the diagram below.
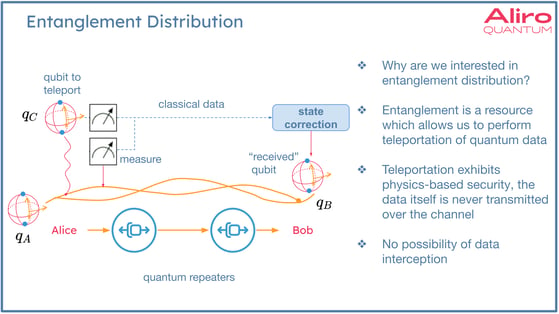
Alice has qubit qA, which has shared entanglement with Bob's qubit qB. To teleport QC, Alice entangles qubit qC with qubit qA, and then performs two measurements. These two bits of classical information are then transmitted to Bob who performs a state correction on qubit qB, and thereby reconstructs the state that qC was in initially into the state encoded in qB. In this way, the state is actually reconstructed instead of directly transmitted. This process is teleportation.
The data is never exposed on the network, and the two bits of classical data are useless unless applied to qB. This creates immunity to man-in-the-middle attacks, or harvest now decrypt later attacks, which is a security benefit of entanglement-based quantum networking.
The way entanglement-based quantum networks achieve provable security is through distributing entanglement across the network to support secure communication or secret-sharing. Quantum repeaters are required to extend the distances between nodes in an entanglement-based quantum network. Quantum repeaters are likely to evolve in capabilities over time:
- In first generation networks, a low entanglement generation rate is expected. Specific protocols are used in generating entanglement, extending entanglement, and improving the fidelity (or quality) of the shared quantum states. QEC would not be used in 1G networks, but a localized, scheduled methodology developed by Aliro Quantum does have useful application in bridging the gap between first generation networks and second generation networks.
- In second generation networks, there is an increase in the bandwidth of the network, or the ability to generate entanglement. This is where introducing entanglement-based error correction can help mitigate some operational errors.
- In the third generation quantum networks, there is a paradigm shift away from entanglement distribution toward a direct transmission of high dimensional encoded states.
Specific protocols are required in order to distribute entanglement across a network.
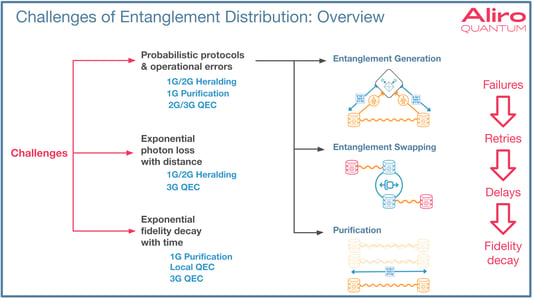
Entanglement generation is the protocol used for point-to-point entanglement, or elementary entanglement generation. This begins with two matter qubits at two nodes. There is synchronized photon emission between these two nodes. The photons are processed by Bell state measurement, consisting of a beam splitter and detector subsystem. When this protocol succeeds, classical information will then indicate when success occurs. When success does occur, entanglement has been established between these two nodes.
Once elementary entanglement is established, it will often be necessary to extend the entanglement across longer distances because the users may not be adjacent to each other on the network. The protocol for achieving this is entanglement swapping, shown above in the middle diagram is a method for doing this. The diagram shows a middle node with entanglement established to the left, and another independent entanglement established to the right node - this is link-wise entanglement. Performing a Bell state measurement operation then transforms these independent entanglements into one longer entanglement that goes end-to-end to the distant nodes.
Lastly, purification is a method for utilizing multiple shared entangled pairs, represented by the light orange part of the final diagram. By performing some specific operations that allow these multiple weaker entanglements to become a single stronger, higher quality fidelity entanglement.
These protocols are all probabilistic - meaning there are failures and retries, resulting delays before success is achieved. During these delays, the quality, or fidelity, of the quantum state decays. In addition to the probabilistic aspects of the protocols, there are fundamental challenges related to distance between nodes. There is an exponential increase in the probability of photon loss in relation to distance. There is an exponential fidelity decay in relation to time as shared states await the next stage of the protocol to run.
Various methods exist that deal with these challenges for different generations of entanglement-based networks.
In first generation networks, the main way these probabilistic aspects are handled is through heralding. Heralding means a classical signal will indicate when the protocol succeeds or fails. For these first generation networks, this information is used to gauge when a retry is necessary. In second generation networks, entanglement-based error correction is introduced to address fidelity drops caused by performing entanglement swaps using the entanglement swapping protocol. In third generation networks QEC is used to mitigate all of the challenges related to these protocols.
Why don't we just use QEC to deal with these errors in first generation entanglement-based networks? The answer is that the error correction used in third generation networks require many more resources to construct large error correcting codes. The first generation networks - and first generation repeaters - simply don't have the resources available to perform this level of error correction, so it’s necessary to leverage these other techniques.
This probabilistic aspect is not only a challenge for generating short distance entanglement; it compounds with longer distances. Success becomes even more challenging when servicing multiple users or multiple connections.
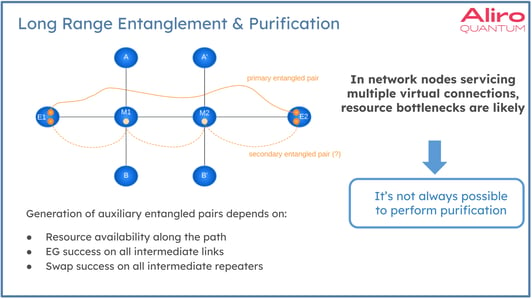
The diagram above shows an example where the two nodes, E1 and E2, have established long distance entanglement. It’s possible in this case that the fidelity is not as high as needed for the application here - whatever the application might be - and so something needs to be done to boost the fidelity. One option for this is entanglement purification. Purification requires an additional entangled pair to be established, which would require multiple entanglement generations and entanglement swaps to establish any additional entangled pairs using resources in the middle nodes M1 and M2. If the middle nodes are also servicing connections, these transverse connections from A to B, during some window of time the resources are simply not available to establish the desired auxiliary entanglement shown in the dashed orange line below. In this example, there will be times when under heavier load, it will not be possible to perform purification or purification will be delayed at the cost of fidelity. Aliro's method of Local-QEC can meet these challenges for early generation networks. Fault-tolerant quantum networking with larger QEC codes will also be able to meet these challenges, but with far more required resources. Entanglement-based error correction can be used to meet these kinds of challenges. What distinguishes Aliro’s Local QEC method from generic QEC is:
- Local QEC uses only local operations to protect previously established entanglement, no need for distributed operations across the nodes
- Local QEC uses compact (small) codes with limited code distance which is compensated by scheduling multiple QEC operations over time
- Local QEC schedules the QEC operations in a specific way to optimize the tradeoff between the QEC benefit and the fidelity cost of the QEC operations themselves (due to gate noise)
Error correction is a broad area of research. It branches outward to many research subdomains. Entanglement-based quantum error correction increases the reliability and scalability of entanglement-based networks, offering a promising avenue for overcoming the challenges posed by noise and imperfections, and enables further evolution of entanglement-based networks. Given this wide range of research into QEC, Aliro has focused on a very narrow part of the overall landscape related to error correction. In the examples of using QEC in this article, a modest number of qubits and a handful of auxiliary qubits are used in maintaining coherent states or coherent shared states. For a deeper look at error correction, and specifically the method developed by Aliro that bridges first generation and second generation entanglement-based networks, please see the on-demand webinar, Scheduling Quantum Error Correction in Entanglement-based Secure Networks.
References
Keith Kenemer, Michelle Chalupnik, Michelle Fernandez, Michael Cubeddu, Eric G. Brown. “Scheduling Compact Error Correcting Codes in Entanglement Distribution Networks.” September 2023. https://dl.acm.org/doi/abs/10.1145/3610251.3610558
Joschka Roffe. “Quantum Error Correction: An Introductory Guide.” July 2019. https://arxiv.org/abs/1907.11157
John Preskill. “Chapter 7. Quantum Error Correction.” Spring 1999. http://theory.caltech.edu/~preskill/ph229/notes/chap7.pdf

