
If you want to understand nature, you need to measure it. The better your measurement, the better you can understand nature. It turns out that building sensors out of quantum objects can yield higher precision measurements. And, even further, a network of quantum sensors can do even better.
Why do we need quantum sensing?
“Nature isn't classical, dammit, and if you want to make a simulation of nature, you'd better make it quantum mechanical, and by golly it's a wonderful problem, because it doesn't look so easy.” -- Richard Feynman
The only way to really talk to nature is to speak in its language—and the language of nature is quantum. The above quote from Feynman, the legendary researcher and professor, is often credited with sparking the race to build a quantum computer. Feynman’s basic realization was that if classical computers have trouble modelling quantum systems, maybe a computer built on a quantum system could outperform a classical one.
This same concept that led to the pursuit of quantum computers explains both the motivation and potential of quantum sensors. If we want to measure the real world with better and better precision—and we do—then we need quantum sensors.
How does a quantum sensor work?
Quantum sensors use quantum systems—like atoms and photons—to measure some quantity in nature with higher precision than can be achieved with a classical sensor.

A single quantum sensor is used to measure the strength of a magnetic field, denoted as θ.
The job of a quantum sensor is the same as that of a classical one -- to learn about some aspect of the world. More concretely, sensors estimate some value in nature. For example, a thermometer estimates the temperature in a room. A compass estimates the direction of the Earth’s magnetic field. In both of these examples, there’s some real value out there: the true temperature or the true direction. But, as anyone who has experienced the frustration of a faulty thermostat would know, sensors often fail to report the true value that they are meant to measure. In fact, sensors are always wrong. Sensors can’t capture the exact value from nature; instead they provide us an estimate. The better the estimate, i.e. the more closely it resembles the true value, the better the sensor. This is referred to as the “precision” of the sensor—a measure of how likely it is to resemble the true value from nature.
A magnetometer is a kind of sensor that is used to measure some aspect of a magnetic field, just as we saw in the example of a compass. Imagine that we want to know the strength of some magnetic field. Let’s call the true strength θ. This is the real value from the world that we want to estimate with our sensor. Then, the output of our sensor will be some value θ̂, which we hope to get as close to θ as possible.
In a quantum sensor, we obtain our estimate, θ̂, using a quantum state. To do this, we can take advantage of the fact that qubits are influenced by the environment. In this case, we create a controlled environment where the thing we want to measure, in this case the magnetic field, is allowed to interact with our measurement qubit. Depending on the strength of the magnetic field, the qubit will react differently. Knowing this, we can then measure our qubit and use the result of that measurement to obtain our estimate of θ.
What if we connect sensors together?: Distributed quantum sensing
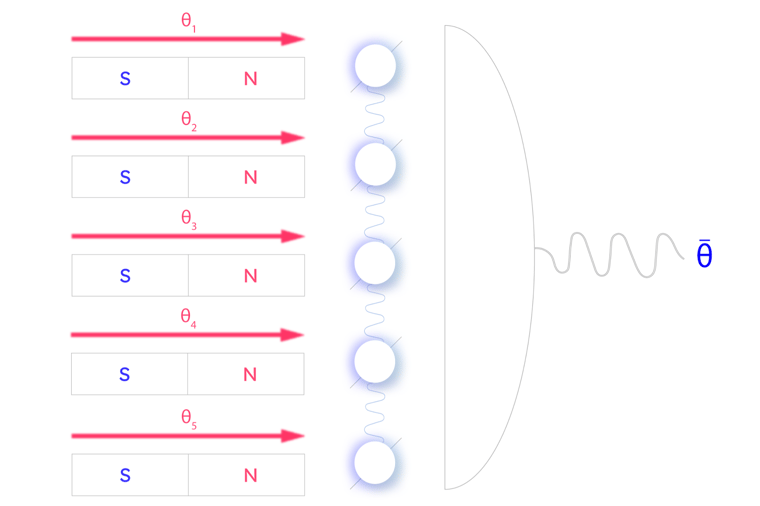
A network of entangled sensors estimates the average θ̄ of a set of parameters θ1 through θ5
So far, we’ve just been talking about problems where we want to know a single value for our measurement, such as the temperature in a room or the strength of a magnetic field. However, often we actually want to measure many values from a system at the same time. This kind of measurement is known as multiparameter estimation. We saw that quantum sensors can achieve improved precision for single parameter estimation problems, and it turns out that networks of entangled quantum sensors can provide an additional advantage for multiparameter estimation.
Imagine we now have 5 magnetic fields that we want to learn about. Each magnetic field has its own true strength value as before. In this case, though, we actually want to know the average strength across all the magnetic fields. One option would be to use our single quantum sensors from before and measure each field, then take the average. However, no matter how good our quantum or classical sensors are, we know there is a mathematical limit to how precise our measurements can be.
By using a network of entangled quantum sensors to measure the inputs, we can achieve better precision than is possible using individual sensors. Using this network of sensors, we can directly measure the average value we are interested in, skipping over the intermediate step of calculating the individual strengths. This method of measurement using a network of entangled sensors is known as distributed quantum sensing (DQS).
Distributed quantum sensing has the potential to reshape a number of industries. Researchers have already proposed exciting potential applications of DQS and more are sure to come as the technology develops. A small subset of examples of what could be possible with DQS include:
- Precise measurement in living systems: In biological applications, sensing capabilities are highly limited by the sensitivity of biological samples to damage. Researchers have found methods of using entangled quantum sensors to enhance precision of measurements without risking damaging the biological system.
- A super accurate global clock: Currently the best clocks in the world, including the one that actually defines the meaning of a second, are built using quantum technology. While these clocks are incredibly accurate already, more precise timing would allow for a variety of applications such as improved GPS. Researchers have proposed a method of building a single global timing system based on a network of entangled quantum clocks. This global network could then even be applied for sensing applications, acting like a huge global sensor.
- Inertial navigation: Inertial navigation is a technology that makes it possible to determine geographic location without needing to connect to an outside source, like GPS. The basic idea is that if you know your starting point and precisely how you moved from that point, you can determine your current location. Distributed quantum sensing allows for better devices called fiber optic gyroscopes (FOG), which can enable precise inertial navigation.
How good is my sensor? Short intro to quantum Fisher information
As the focus of quantum sensing and distributed quantum sensing is to develop better sensors, it’s an obvious question to ask how to check the quality of a given sensor. To do this, researchers rely on a quantity called the “quantum Fisher information” (QFI). While we won’t get into the details in this post, intuitively, QFI is a measure of the precision of a sensor. A sensor with a high QFI is able to extract more information from what it wants to measure and so has higher precision. On the other hand, a sensor with a low QFI is lower quality and has lower precision.
It turns out that it’s hard to compute the QFI of a sensor directly. This is a problem, because in practice we want to know how good we can expect our sensor to be. To get around this, researchers have developed methods of bounding the QFI, so that you can at least determine a range within which the true QFI will be. For example, in single parameter estimation problems, measures such as sub-QFI and TQFI can give lower bounds for the true QFI. In fact, researchers have also developed methods of measuring these bounds efficiently using techniques on near term quantum computers.
What’s next?
We’ve just covered the very tip of the iceberg in the field of distributed quantum sensing, which is rapidly evolving. In future posts, we will dive deeper into specific areas, like QFI and its bounds, and follow the latest research as it develops. If you’d like to better understand quantum Entanglement as a Service and its applications, you can sign up for Aliro’s monthly newsletter, which covers the latest developments in quantum networking each month.
Acknowledgements
Thank you to Akira Sone for his help in this introduction to distributed quantum sensing!
